
I thought it might be nice to reflect on the physics that I am most interested in understanding during this second run of the Large Hadron Collider (LHC). In this post, I will discuss the Higgs boson, its expected interaction with bottom quarks, and how we have come to understand this interaction (in part) during Runs 1 and 2 of the LHC. The Higgs Boson and the Bottom Quark have a close relationship. Whilethe bottom quark was found during the “glorious discovery period” of the 1970s and 1980s, and the Higgs boson was found in 2012, we have not yet a definitive direct measurement of the Higgs and Bottom Quark interaction. I am working with my colleagues to change that fact. But to understand where we are, it’s helpful to understand where it all comes from.
Meter Sticks
Let’s begin by defining some meter sticks. These are helpful numbers that give us a sense of things. For instance, let us think about a hydrogen atom. A hydrogen atom, two of which are present for every one oxygen atom in a water molecule, is itself composed of two particles: the proton and the electron. For the most part, the mass of the hydrogen atom can be explained by the sum of the masses of the proton and the electron. But the proton and the electron are very different particles. The electron has a mass that is almost 2000 times smaller than that of the proton. So, really, the mass of the hydrogen atom is mostly explained merely by the mass of the proton.
Particle physicists use “funny units” to describe mass, because mass in the world of people (conveniently described by the kilogram – there are 2.2 lbs in every kilogram) is of a very different scale than mass in the world of subatomic particles like the proton and the electron. The kilogram is just not convenient for describing that tiny world, so we instead use “electron-Volts” – specifically, the mass of the proton in particle physics units is very conveniently 1 billion electron-Volts, written as “1 GeV” for “1 Giga-electron-Volts”. The proton mass will be our meter stick for masses in the subatomic world. As I said, the electron’s mass is about 2000 times smaller than that of the proton, or about 0.0005 GeV. In comparison, an atom of gold (a huge composite of neutrons, protons, and electrons) has a mass of about 183 GeV, or about 183 times that of the proton.
The Particle Zoo
The electron was the first subatomic particle discovered, and it was found by a scientist named J. J. Thompson in 1897. The proton was discovered almost a decade later, and the neutron (which is part of all other atoms except hydrogen) was discovered almost 40 years later. The period that unfolded after the discovery of the last component of stable atoms was a golden era of new, seemingly fundamental, building blocks of nature. They came with many names: muons, pions, kaons, lambdas . . . all the Greek letters seemed to be taken by new subatomic particles. This was a confusing period, and many physicists struggled to find the pattern in all of this discovery.
When the dust settled . . . and it really didn’t settle until the 1970s . . . a very good explanation emerged for most of these other particles that had been discovered. Pions, kaons, lambdas . . . even protons and neutrons . . . they could all be explained if there were a new kind of even more fundamental particles, dubbed “quarks”, that composed these states of matter. Evidence for the quark hypothesis was scant at first, but experiments in the 1960s revealed that the proton and neutron were indeed made of something more fundamental. At first, three quarks, called “up,” “down,” and “strange,” seemed to be all that was needed to explain this particle zoo. But the quark hypothesis started to show predictive power in the 1970s when it was suggested that the existence of at least a fourth quark, dubbed “charm,” would neatly explain some other observed features of nature that had nothing to do with new particles, but rather the behavior of those found in the 1930s-1960s.

Evidence for the Charm Quark was first obtained in November, 1974, when two teams (one at Brookhaven Laboratory in Long Island, NY, and the other at the Stanford Linear Accelerator Center in California) reported evidence for a new state of matter whose existence was incompatible with just the up, down, or strange quark, but could be explained by a fourth quark. An independent team in Italy confirmed the observation of this new particle, the “J/psi”, that was seen as a herald of the Charm Quark’s existence. But, it wasn’t until the discovery of additional states of matter made from just one Charm Quark paired with an Up or a Down Quark that the existence of the Charm Quark was considered settled science.
Of course, if you can have four quarks . . . why not five? Evidence for this idea was further provided by the fact that a system of particles parallel to the quarks – the leptons, whose poster child is the electron – seemed to have three generations of particles, each heavier than the last. Arranged similarly, the Up and Down Quark formed the lightest “generation” of quarks; the Strange and Charmed Quark formed the second generation; a third generation, to parallel that of the leptons, seemed like a natural idea. The hunt was certainly on, regardless.
Enter: Bottom
The bottom quark is the second-heaviest known building block of nature. Comprised of a mass-energy that is a little more than 4 times that of the proton, it also possesses electric charge and is charged under the strong and weak interactions as well. Like all quarks, the bottom quark “feels” the presence of other building blocks of nature through all of the four known forces of nature. It can interact using photons via the electromagnetic interaction, using gluons via the strong interaction, and using weak bosons (the W and Z) via the weak interaction. Since the bottom quark possessed mass-energy, it can warp space-time like anything else with energy can do; however, this warping is so small that the force that results (gravity) is extraordinarily weak compared to the other three forces, and for all intents and purposes the gravitational force appears to play no serious role in the behavior of bottom quarks.
Bottom quarks can bind with other quarks for form states of matter, like “bottomonium” (the binding of a bottom quark to a bottom anti-quark) or “B mesons” (the binding of a bottom quark with an up, down, charm, or strange anti-quark). Being the second-heaviest building block of nature, and the heaviest one with a mass below that of the Higgs Boson, it is expected to have a special relationship with the Higgs. The Higgs boson’s interactions with other particles is proportional to the square of their masses; since the bottom quark is so heavy, it’s expected to be something with which the Higgs boson will frequently want to interact.
Higgs and Bottom
The Standard Model of Particle Physics makes very specific predictions about the interaction strength of the Higgs boson and the bottom quark. The key prediction that matters to me is that the probability that, if a Higgs boson decays, that it will decay into a pair of a bottom quark and a bottom anti-quark, is about 60%. The LHC Higgs Cross-Section Working Group has collected together the most precise predictions of this process, and the number comes out to be exactly
(58.09 +/- 1.25) % (for a Higgs mass of 125.09 GeV)
This is big. This is huge! The decay of the Higgs boson to a pair of bottom quarks is the single-largest decay probability of the Higgs to any final state. So, you’d think it would be easy to find. It is not.
Evidence for this process is crucial to a complete understanding of the Higgs boson, but we cannot see the bottom quarks directly when they are produced. Like all quarks, they interact so strongly that they create sprays of particles in our detectors, call “jets”. The problem with this is not that we are not good at reconstructing and even identifying kinds of jets. The problem is a numbers game: the LHC produces so many jets that asking for two bottom-quark-like jets from a proton-proton collision in the LHC is akin to trying to find a specific person knowing that they have blue eyes. You can be very good at spotting blue eyes, but if that’s all you can do then the sheer rate of false positives you will get by looking for a specific person by walking up to strangers and looking at their eye color will swamp you.
To find the Higgs boson decaying in this way, given the sheer rate at which the LHC produces jets (and even bottom-quark-initiated jets), we have to be choosier. We have to look for specific ways that the Higgs itself was produced that limits the number of jets that should be present, and cuts down on all those proton-proton collisions that make jets but without the presence of a Higgs. The way I have been doing this with my colleagues in Run 2 of the LHC is to ask that the Higgs be produced along with a weak boson – a W or a Z – which then decays to leptons (e.g. electrons, muons, and neutrinos). This works amazingly well to suppress the noise rate in the LHC. It still leaves us with challenges, but this is why you assemble a team of outstanding people – to solve the problems one at a time so you can chip away at the remaining noise and see if there is any signal left to study.
Lessons from the data
What we have learned so far, from both data taken during Run 1 (where I was not involved in this analysis) and in Run 2 (where I have been involved in this analysis) is so-far puzzling. You don’t want to read into this too much, but the statistician in me is frustrated that (should all of this just be unluckiness) we have been unlucky twice in the ATLAS Experiment (I’ll talk about our competition, CMS, in a moment).
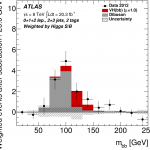
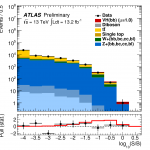
The puzzle becomes a bit clearer when we then ask the following question: compared to what the Standard Model predicted we would see with this much data, how did our observations compare? We call this ratio – observed-to-expected – “μ” and I show the results from the ATLAS Experiment in Run 1 (top) and Run 2 (bottom) below.
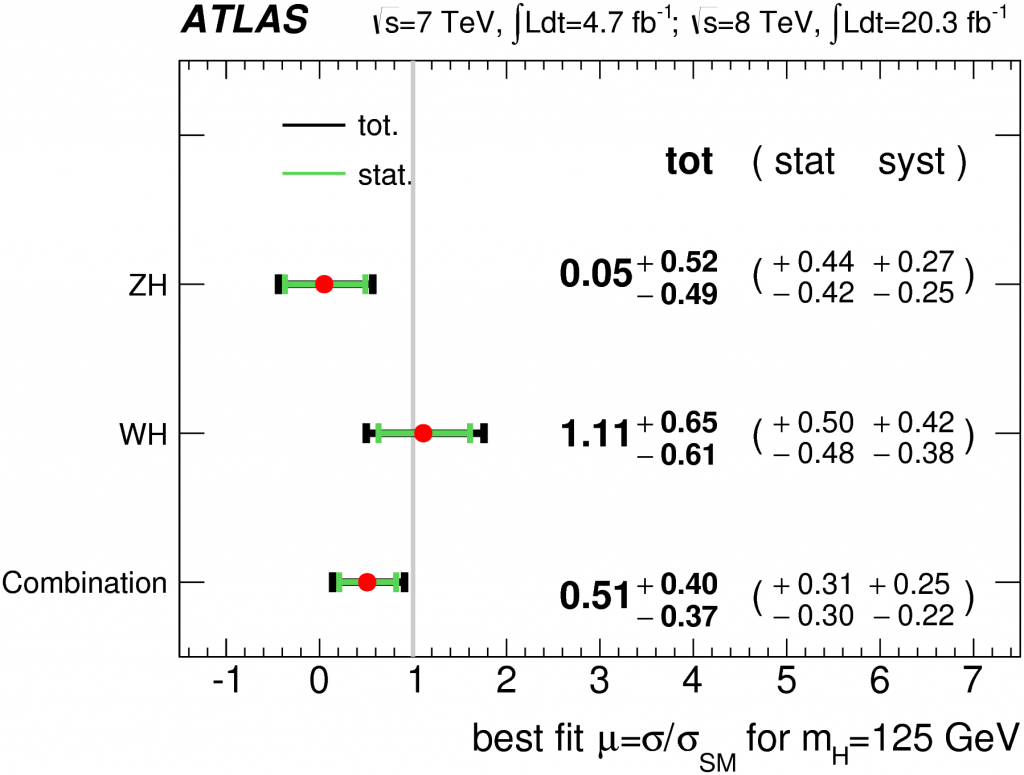
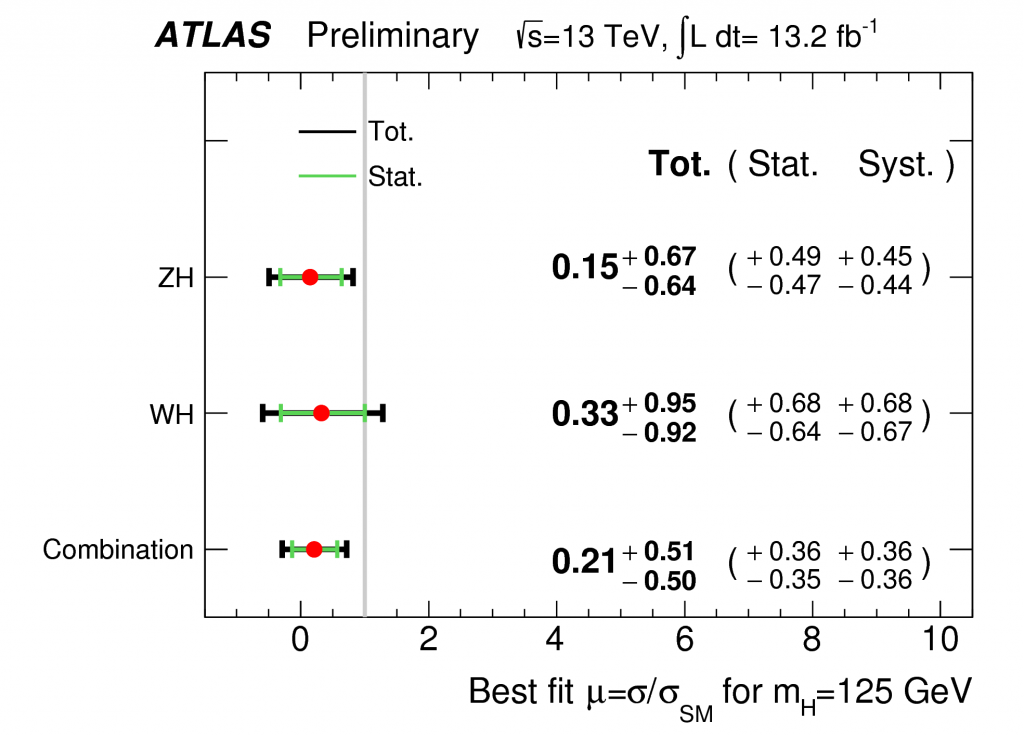
In Run 2, we have only so far analyzed about half the data taken this year at the LHC by the ATLAS Experiment; the rest will be analyzed as the year continues. That said, the data we have analyzed already is approaching comparability in sensitivity to the data from Run 1, even if in absolute data-measurement units (inverse-femtobarns, or /fb) we have a lot less data to use. Data taken in Run 2, at a higher LHC energy, is worth more than the equivalent unit of data from Run 1. So what do we see?
We see something similar to what we saw in Run 1. We observe a result compatible within uncertainty with the Standard Model but also with non-existence of this process. However, the uncertainties are large. Taken literally, the rate at which we observed this process so far in Run 2 is 21% that of the Standard Model prediction… but, again, here we have large errors.
No, no, no… don’t do that. Wait. Never mind.
An extremely naive and ill-advised private back-of-the-envelope combination (using simple error-weighted average and treating the two measurements as totally uncorrelated… dumb dumb dumb with two numbers from the same experiment…!) of the Run 1 and Run 2 (so far) ATLAS results yields a value for the ratio of observed-to-expected of (0.39 +/- 0.31). Assuming this is a Gaussian uncertainty (doubly naive), this is compatible with the Standard Model just within 2 standard deviations. Again, not much to write home about here. We haven’t ruled in or ruled out the Standard Model… this is inconclusive, at best. Keep calm, and collect more data.
I love studying the Higgs. There is clarity of purpose for a particle physicist and a new particle has been discovered. The Standard Model makes definitive predictions. Test them. Do it methodically. Be creative. Make improvements to try to be more clever than people thought was possible. It’s very satisfying. But it will be even more satisfying to use more of the data we already have, and all of the data yet to come, to overwhelm this difficult analysis with the cleansing light of data.
CODA
What about our competition, the CMS Experiment? What have they seen?
In Run 1, CMS saw an observed-to-expected ratio that was higher than what ATLAS saw, but no better at discriminating between the Standard Model or a non-observation given the errors on their measurement: 1.0 +/- 0.5. [4]
What about in Run 2? So far, regarding this search channel, they have no preliminary or published results that I could find. I am certainly eager to see what they have found with whatever data they can use to search.
References
[1] c.f. http://history.fnal.gov/botqrk.html
[2] The ATLAS Collaboration. “Search for the bb decay of the Standard Model Higgs boson in associated (W/Z)H production with the ATLAS detector”. J. High Energ. Phys. (2015) 2015: 69. doi:10.1007/JHEP01(2015)069. http://link.springer.com/article/10.1007/JHEP01(2015)069
[3] The ATLAS Collaboration. “Search for the Standard Model Higgs boson produced in association with a vector boson and decaying to a bb pair in pp collisions at 13 TeV using the ATLAS detector”. ATLAS-CONF-2016-091. https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2016-091/
[4] The CMS Collaboration. “Search for the standard model Higgs boson produced in association with a W or a Z boson and decaying to bottom quarks”. PRD 89 (2014) 012003, http://cms-results.web.cern.ch/cms-results/public-results/publications/HIG-13-012/index.html
[5]




