A little bit of math: vaccine efficacy

With reports from Pfizer/BioNTech and Moderna that the preliminary analysis of their data suggests a 95% effective vaccine (one each for each company) [1], I found myself wondering about the mathematics of vaccine effectiveness. There were some small details about how numbers were calculated from the data that were lost to me. This weekend, I had some time to think a little about those details. While I can’t claim to understand everything, I certainly understand a few things much better. I want to share that here.

First, we need some basic numbers to guide our calculations. Let’s use the basic sketch of the Moderna trial to inform us. Moderna is following what appears to be a gold-standard approach for testing a medical claim: they gather a large group of participants an randomize them into two groups. One group (the control group) received a placebo. The other receives the vaccine candidate. The administration of the placebo (appearance, method of introduction, etc) must be identical in all possible ways so that doctors and patients cannot guess which they are getting. The patients do not know which group they are in, nor do the people administering their treatment. This is “double-blind” so that no influencing of the patient’s beliefs can occur.

The two vaccine trials appear to have similar approaches. In each case, they divide their pool in half, one half for the control and one for the vaccine. The Moderna trial has about 15,000 people in each group.

Preliminary results from the trial report that 95 people overall have developed COVID-19. 90 of them were in the control group. 5 were in the vaccine group.

Here is where things got confusing for me. This trial is NOT a challenge trial. In a challenge trial, a number (half, maybe all) of the participants would be intentionally exposed to SARS-CoV-2. This “guarantees” that you know for a fact that all participants were equally exposed to the virus. As you can imagine, this is fraught with ethical peril. Instead, the Pfizer and Moderna trials rely on their participants simply going about their lives with each person potentially exposed to SARS-CoV-2, but at an unknown rate of exposure. Some people might never socialize, avoid going out, etc. Some people might be quite gregarious. How do the scientists running the trial know the level of exposure received by patients? That would seem to be essential to determining vaccine effectiveness (e.g. I know patient A was definitely exposed to SARS-CoV-2, so if they got the vaccine and didn’t develop COVID-19 I might be able to make a statement about the effectiveness of the vaccine; but if they were never exposed, the fact that they didn’t develop it would be unremarkable).

Thankfully, epidemiologists have wrestled with this problem for a long time. The concept of “Vaccine Efficacy” has emerged to help us sort out the signal from the noise.

Vaccine Efficacy

The mathematical definition of vaccine efficacy stems from a comparison of the risks that each group – vaccinated ( $V$ ) and unvaccinated ( $\overline{V}$ ) – experience when out running their lives in the presence of SARS-CoV-2. It’s a calculation of the relative risk of the two groups.

The risk of a person who is vaccinated, also being infected, is given by the conditional probability $P(I|V)$ (to be read, “the probability that a person is infected, given that they are vaccinated”). Similarly, the probability that a person is infected given that they are unvaccinated is $P(I|\overline{V})$ . Each of these represents the risk of people in each group – control and vaccine – getting sick.

We can visualize these populations.

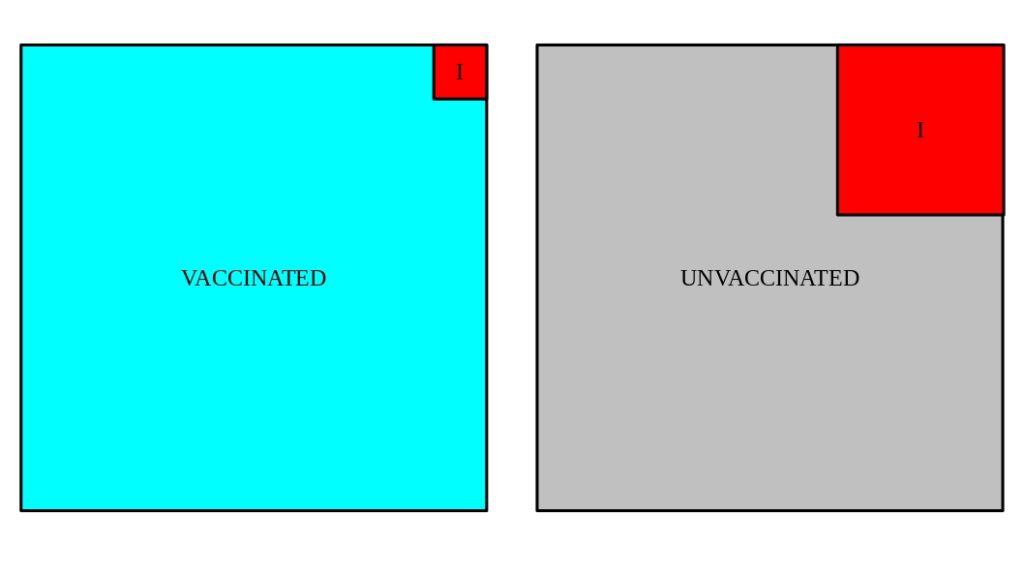
An exaggerated representation of the infected sub-populations (I) of the two groups, vaccinated and control (unvaccinated).

What isn’t visible in these cartoons are the ingredient that we would really LIKE to know … the number of people in each group that were exposed to SARS-CoV-2 in sufficient quantities that they should have become infected (e.g. tested positive and/or developed symptoms).

A key assumption in these studies – one which is intentionally controlled by the scientists who construct the study, albeit without a guarantee of perfection – is that the two populations are overall similar, though randomized. They would consist of similar age, ethnicity, etc. demographics. In addition, they would have similar geographic and potential exposure demographics. That would guarantee that regardless of what the exposure rate is, it’s the same for participants in both groups.

Still, we cannot know it. So we have to construct a measure that doesn’t depend on it … one where the unknown, but assumed-to-be-consistent exposure rate simply cancels out of the equation. That turns out to be what is known as “vaccine efficacy”:

$\varepsilon = \frac{P(I|\overline{V}) -P(I|V) }{P(I|\overline{V})} = 1 - \frac{P(I|V)}{P(I|\overline{V})}$

The risk of developing COVID-19 is never exactly zero, even when vaccinated. So the meaningful measure, one which cancels out (completely, or even mostly) the unknown exposure rate, is the relative risk of infection to the two populations.

For instance, if the risk is the SAME for both groups, this is the special case that $P(I|V)=P(I|\overline{V})$ . In that case, $\varepsilon=0$ . In other words, the vaccine makes no difference – it has zero effect on the relative risk.

But in the Moderna trial, we know from the data that $P(I|V) = 5/15,000 = 3.33 \times 10^{-4}$ . We also know that $P(I|\overline{V}) = 90/15,000 = 60 \times 10^{-4}$ . Thus the vaccine efficacy is $\varepsilon = 1 - \frac{3.33}{60} \times 10^{-4} = 0.944$ , or 94.4%. This is where the statement that the “vaccine is 95% effective” comes from.

But what about the exposure rate?

What if the exposure rate is NOT the same between the two groups? This would mess up the conclusion, of course – it would be a “systematic uncertainty,” because it would be impossible to guarantee its effect is zero. The construction of the study, making sure the demographics of the two groups (control and vaccinated), would be the best guarantee … but it can’t ever be absolutely perfect.

This is part of the natural uncertainty built into studies like this. However, with a large enough group it should be possible to greatly reduce the harm of such a systematic effect. The fact that two very different vaccines being tested in two very independent trials both seem to have a very high efficacy suggests this effect has been well-controlled so far.

Statistical Uncertainty on the Efficacy

The efficacy itself is not sufficient information to make public health decisions. One needs to also factor in the reality that in the preliminary data only 5 people in the vaccine group got COVID-19 … a very small number, with a very large statistical (Poisson) uncertainty, $\sigma = \sqrt{5} = 2.24$ . That’s a relative uncertainty on the number of infected persons of $\sqrt{5}/5=0.45$ , or a 45% relative uncertainty. Could such large uncertainty cloud the efficacy evaluation?

It’s important to state first that the vaccine trials always had at least 2 checkpoints in their procedure. The first checkpoint was the one we hit and resulted in the “95% efficacy” announcement … the second checkpoint is triggered when the total number of infections in the groups exceeds a certain number, about double that in the first checkpoint. So the scientists running the trial recognized that it was important to keep accumulating data to reduce statistical (and potentially systematic) uncertainties.

How do we take the raw counts – 95 total infected people – and translate that into an uncertainty on the efficacy? We need only employ the same error propagation techniques (addition of errors in quadrature using calculus) taught in introductory physics labs to answer this question.

The efficacy involves the ratio of two uncorrelated numbers. How many people get sick in the vaccine group has nothing to do with how many people get sick in the control group. These are statistically uncorrelated numbers. Therefore, we can use simple error propagation for two uncorrelated variables, $x$ and $y$ , to answer the question. Rewrite the efficacy as:

$\varepsilon = 1 - \frac{x}{y}$

First, we write the sum in quadrature of the uncertainties on the efficacy due to the two infected yields, $x$ and $y$ . For this, we need calculus and the chain rule:

$d\varepsilon^2 = \left( \frac{d\varepsilon}{dx} \right)^2 dx^2 + \left( \frac{d\varepsilon}{dy} \right)^2 dy^2$

Let’s compute each derivative:

$\frac{d\varepsilon}{dx} = -\frac{1}{y}$

$\frac{d\varepsilon}{dy} = -\frac{x}{y^2}$

Putting these back into the quadrature equation:

$d\varepsilon^2 = \frac{1}{y^2} dx^2 + \frac{x^2}{y^4} dy^2$

Since $x$ and $y$ are counts (5 and 90, respectively), and the uncertainty on counts in an experiment are determined by random error and thus Poisson statistics, we can write $dx = \sqrt{x}$ and $dy = \sqrt{y}$ . Therefore

$d\varepsilon^2 = \frac{x}{y^2} + \frac{x^2}{y^3}$

This can be further simplified to

$d\varepsilon^2 = \frac{x^2}{y^2} \left(\frac{1}{x} + \frac{1}{y}\right)$

We can now solve for the uncertainty on the efficacy:

$d\varepsilon = \sqrt{\frac{x^2}{y^2} \left(\frac{1}{x} + \frac{1}{y}\right)} = 0.0255$

Thus, based solely on the statistical uncertainty we can say that from the preliminary data the vaccine efficacy is known to be $(94.4 \pm 2.6)\%$ .

Despite the very small number of infected in the vaccinated group, we nonetheless know the efficacy quite well. Treating this uncertainty, as is typical in counting statistics, as the 68% confidence interval, we can estimate that the true value of the vaccine’s efficacy has a 68% change of being somewhere in the range $\varepsilon_{68}=[91.8, 96.9]\%$ . The 95% confidence interval is obtained within range of two standard deviations, so $\varepsilon_{95}=[89.3, 99.5]\%$ – that is, there is a 95% chance that the true efficacy lies somewhere in this range.

Obviously, more data will improve this situation. For example, Moderna will reach their next checkpoint in the study when the total number of infected persons reaches 151. Assuming the proportion of people in the control and vaccine group remains the same over time, that results in 8 infected persons in the vaccine group and 143 in the control group. In that case, the uncertainty on the efficacy will be 2.0%.

References

A summary of both vaccines: https://www.washingtonpost.com/health/2020/11/17/covid-vaccines-what-you-need-to-know/?arc404=true
More on the Moderna vaccine: https://www.washingtonpost.com/health/2020/11/16/covid-moderna-vaccine/

A little bit of math: vaccine efficacy

Vaccine Efficacy

But what about the exposure rate?

Statistical Uncertainty on the Efficacy

References

AUTHOR

steve

Vaccine Efficacy

But what about the exposure rate?

Statistical Uncertainty on the Efficacy

References

Related posts:

AUTHOR

steve